We can rely on the historical (or realized) average return when evaluating an asset’s past performance. In that sense, the historical average return is a backward-looking measure. But, to forecast an asset’s future performance, we need a forward-looking measure. This measure is called the expected return. In this lesson, we explain how to compute the expected return of a risky asset and offer an online calculator as well.
Contents
Expected return calculator

When using our expected return calculator below, please pay attention to the following points:
- Please ensure the probabilities add up to 100% (the sum of the probabilities is given in the final row).
- If your calculation requires, say, 3 states only, simply leave 0s in the fields involving the states 4, 5, and 6.
- Returns can be positive, negative, or zero.
You may also find the following calculators useful:
Expected return formula
Formally, the expected return formula can be written as follows:
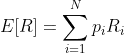
This means that E[R] is a probability-weighted average of all possible return outcomes where pi is the probability of the ith state and Ri is the risky asset’s return under state i.
Let us illustrate the use of this formula with an example. Hillary has savings worth $5,000 and is considering investing in the U.S. stock market. She believes the market will be in a “good state” with a 60% probability and a “bad state” with a 40% probability next year.
Hillary is interested in a specific stock that yields 10% when the market is in a good state and down and −5% when the market is in a bad state. Using the expected return formula, Hillary finds that:
E[R] = 60% * (+10%) + 40% * (−5%) = 4%
This means that if Hillary invests $5,000 in the stock today, the expected value of her investment in one year is:
$5,000 * (1 + 4%) = $5,200
What if there were three possible states instead of two as follows?
| State | Probability | Return |
| 1 | 50% | +10% |
| 2 | 30% | −5% |
| 3 | 20% | 2% |
Then, we would have:
E[R] = 50% * (+10%) + 30% * (−5%) + 20% * (2%) = 3.9%
And, we would expect the value of the $5,000 investment to become $5,000 * (1 + 3.9%) = $5,195 after a year.
Of course, these are stylized examples. In reality, there are not just two or three possible outcomes but many of them, and it is difficult to know the probability associated with each outcome. And, because of that, we normally rely on asset pricing models such as CAPM and APT to estimate expected returns. We will be covering these models in the final part of this course.
Video summary
Summary
In this lesson, we have shown that the expected return formula for a risky asset is based on (i) the asset’s returns under different states of the market, and (ii) the probabilities of those states occurring. We have also offered a handy expected return calculator, which can accommodate up to six different states.
Further reading:
Black (1993), ‘Estimating expected return‘, Financial Analysts Journal, Vol. 49(5), pp. 36-38.
What is next?
This lesson is part of our free course on investments.
- Next lesson: We will discuss the risk-free rate of return.
- Previous lesson: We explained the concept of return volatility.
We hope you find our expected return calculator useful. If that is the case, feel free to share this post with others on social media or other platforms.
If you have got any questions or comments, you can reach us here.

