When investors buy securities (e.g., stocks), they may hold them for months or years before selling them. The duration during which an investor holds on to a particular security is known as the holding period and the return over that period is referred to as the holding period return. This is typically abbreviated as HPR.
Contents
Holding period return calculator
We offer a holding period return calculator that accommodates up to 10 periods (10 months, 10 years, etc.). All you need to do is to enter the return observations for each period. Please note the following:
- If you have, say, 7 return observations, simply leave the fields for Return 8, Return 9, and Return 10 as zero.
- Make sure to enter “net returns” rather than “gross returns”. For example, if the gross return is 120%, then the net return is 20%, so you should enter 20%.
- The result is shown at the bottom, together with the number of (non-zero) return observations you’ve used.
Holding period return formula
Imagine that you bought a stock for £5/share in September. Afterward, the share price increased to £8 in October but went back down to £5 in November. What is your holding period return (HPR) over this 2-month period?
Intuitively, you know that the result should be zero because you bought the stock for £5 back in September and it is still worth £5 in November. In general, you can calculate the HPR as follows:
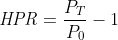
where P0 is the initial price you paid when you bought the stock and PT is the final price you received when you sold the stock. So, we have:
HPR = £5 / £5 — 1 = 0
However, this simple formula works ONLY IF there were no dividends and/or stock splits during the holding period. Otherwise, there are two ways of handling such events as explained next.
Option 1: Use adjusted prices
The first option is to use what we call adjusted prices, which account for dividend payments and stock splits. Various data providers such as Yahoo! Finance offer free access to adjusted stock prices. If you’re using adjusted prices, you can still use the same formula for HPR computations:
HPR = PT / P0 — 1
Now, P0 is the adjusted price you paid when you bought the stock and PT is the adjusted price when you sold it.
Option 2: Compound returns to obtain the holding period return
If you are unable to use adjusted stock prices, you can use the following formula instead.
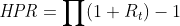
With this formula, we first compute the return for each period and then compound them to get the result. Note that ∏ is the product symbol and is telling us to compound gross returns (1 + Rt ) to obtain the HPR.
Going back to our example, the net return for October is £8 / £5 − 1 = 60% and the one for November is £5 / £8 − 1 = −37.5%. Then, we have:
HPR = (1 + 60%) (1 − 37.5%) − 1 = 0
This is the same result as before.
Video summary
The relevant section on HPRs starts at 08:07.
Summary
In the case of adjusted prices, the HPR is simply the return computed using the adjusted purchase price and the adjusted selling price. In the case of raw returns, you have to first compute the gross return for each period (taking into account dividends, etc.) and then compound these returns to obtain the result.
What is next?
This lesson is part of our free course on investments.
- Next lesson: We will introduce the arithmetic average return as a simple metric for evaluating average investment performance across multiple periods.
- Previous lesson: We discussed the difference between nominal returns and real returns.
Feel free to share this post if you enjoyed reading it. Also, if you noticed any errors or have any suggestions/questions, you can contact us here.

