The topic of this lesson is the return volatility of risky assets such as stocks, mutual funds, etc. We will explain how to measure it and provide a calculator as well.
Contents
What is (stock) return volatility?
Imagine an investor who bought shares of a stock three years ago. According to the investor’s calculations, her annual returns were 7%, 2%, and −3% over this period. Therefore, her average realized return RA is:
RA = (7% + 2% − 3%) / 3 = 2%
While this figure gives the investor an idea about the average yearly performance of her investment, it doesn’t tell her anything about its riskiness.
For that, we rely on return volatility, which captures how risky (or volatile) the returns are. It is computed as the standard deviation of returns, which is the square root of the variance of returns. Variance and standard deviation are two important statistical measures, which are also used in many areas other than finance (e.g., healthcare, quality control, construction, weather forecasting, etc.). Intuitively, these are measures of dispersion, quantifying how spread out the returns are.
Return volatility formula
In order to compute realized return volatility, we begin with the variance of realized returns, or simply the realized variance. The realized variance is the sum of squared deviations from the average realized return RA:
Realized variance = ∑ (Rt − RA)2/ T
where ∑ is the summation symbol, Rt is the return in period t, and T is the number of periods (e.g., months, years, etc.).
Then, we can write the return volatility formula as the squared root of the realized variance, which is of course the same as the standard deviation of realized returns:
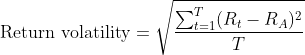
Technical note: If the goal is to estimate future volatility, divide by T−1 instead of T to obtain an unbiased estimator.
If we return to our earlier example, we calculated the investor’s average realized return as RA = 2%. Now, we can compute the realized variance as follows:
Realized variance = [(7% − 2%)2 + (2% − 2%)2 + (−3% − 2%)2] / 3= 0.00167
Finally, we can easily calculate realized volatility by taking the squared root of realized variance:
√(0.00167) = 0.0408 = 4.08%
Now, our investor has a more complete understanding of the stock’s past performance: In the past three years, the stock had an average return of 2% with a volatility of 4%. This helps the investor compare this stock’s performance with similar investment opportunities she had three years ago to determine whether the stock performed relatively well.
Return volatility calculator

Instructions for using the return volatility calculator:
- Enter return observations as percentage points (e.g., enter 10 for 10%).
- You can enter up to 12 observations. When entering fewer observations, say 5, use the first five fields (Return 1, Return 2, …, and Return 5) and leave the remaining fields empty.
- There are three figures reported at the bottom row. If you need an estimate for future volatility, you can rely on the first figure, which divides the sum of squared deviations by T-1. If you’re simply interested in the realized volatility, you can focus on the second figure (T). The third figure is the average realized return, which is given for your convenience.
Video summary
Summary
In finance, we often say that risk and return are the two sides of a coin. Therefore, metrics such as arithmetic average return and geometric average return are helpful when evaluating the past performance of an investment but are not sufficient on their own without proper consideration of risk.
In this post, we have introduced return volatility as a useful risk measure and have derived its formula, relying on the statistical measures of variance and standard deviation.
Further reading
Andersen et al. (2001) ‘The distribution of realized stock return volatility‘, Journal of Financial Economics, Vol. 61 (1), pp. 43-76.
What is next?
This lesson is part of our free course on investments.
- Next lesson: We will move on to forward-looking measures of investment performance and will introduce the concept of expected return.
- Previous lesson: We discussed how geometric average return can be used to assess investment performance and how it differs from the arithmetic average return.
We hope you enjoy reading our content. For any queries or comments, you can reach us here.

