Real return vs nominal return: How do they differ from one another? Suppose that an asset yields a return of 50% over a year. So, if you invest $10,000 today, your investment grows to $15,000 by the end of the year. Sounds not too bad, right? But, imagine that the inflation rate over the course of the year was 60% (this is highly unlikely in most economies, but just imagine). Then, the asset no longer looks so appealing as the return it offers fails to keep up with the rate of inflation!
In this post, we explain the difference between real and nominal returns and show you the impact of inflation on return calculations. You will also learn how to calculate the real rate of return using the nominal rate of return and the inflation rate.
Jump to:
How does inflation affect returns?
Inflation can be loosely defined as an increase in the prices of goods and services. The problem with a high rate of inflation is that it leads to a significant loss in purchasing power.
Let’s illustrate this with a simple example. Suppose that a luxury hot tub costs $5,000 today. This means that with your $10,000 investment, you could afford 2 hot tubs today. And, if your investment grew to $15,000 at the end of the year, you would be able to buy 3 hot tubs if the price of the hot tub didn’t change. But, if its price rose in line with the inflation (60%), it would now cost $8,000. This means that you would actually not be able to purchase 2 hot tubs at the end of the year, while you could at the start…
As a result, one needs to take into account the rate of inflation (especially when it’s high), when interpreting investment returns.
Real return vs nominal return and their relation to inflation
In general, we refer to the rate of return that is unadjusted for the rate of inflation as the nominal return and the one that is adjusted as the real return. So, in our example, the nominal return is 50%. But, how do we calculate the real return, given that the inflation rate is 60%?
The relation between the nominal return Rn, real return Rr, and the inflation rate I is governed by the following equation:
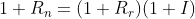
If we plug Rn = 50% and I = 60%, we get:
1 + 50% = (1 + Rr)(1 + 60%)
1.5 = (1 + Rr)(1.6)
Rr = 1.5 / 1.6 − 1 = −6.25%
This means that while the asset offers a quite high nominal return (50%) because the inflation rate is even higher (60%), we would lose money in real terms (−6.25%) if we invested in this asset.
However, if the inflation rate was low, say 2%, the asset would offer a very attractive real rate of return:
1 + 50% = (1 + Rr)(1 + 2%)
1.5 = (1 + Rr)(1.02)
Rr = 1.5 / 1.02 − 1 = 47%
Note that so long as the inflation rate is positive, the real return is always smaller than the nominal return as it accounts for the rate of inflation.
When the rate of inflation is low, the real return is approximately the difference between the nominal return and the inflation rate (the Fisher equation):
Rr ≈ Rn − I
So, when the inflation rate is 2%, we have:
Rr ≈ 50% − 2%
Rr ≈ 48%
This is indeed close to the exact figure of 47% we calculated above.
Summary
The presence of price inflation in an economy forces us to take that into account in our return calculations. And, that leads to the following distinction: Real return vs nominal return. While nominal returns are unadjusted for inflation, real returns are. Moreover, the latter can be much lower than the former when the inflation rate is high. If you are interested in learning more about the distinction between nominal returns and real returns, you can check the further reading below.
Further reading on real return vs nominal return:
Crowder and Hoffman (1996) ‘The Long-Run Relationship between Nominal Interest Rates and Inflation: The Fisher Equation Revisited‘, Journal of Money, Credit and Banking, Vol. 28 (1), pp. 102-118.
What is next?
This lesson is part of our free course on investments.
- Next lesson: We will explain how to calculate holding period returns when assets are held over multiple periods.
- Previous lesson: We covered basic return calculations, introducing concepts such as gross return and net return.
Please share this post with your friends and connections if you enjoyed reading it. Also, please contact us if you noticed any errors or have any suggestions/questions.
