An arbitrage opportunity arises when an asset is mispriced, giving traders a chance to make money. In the case of pure arbitrage, the opportunity carries no risk. The same can’t be said for statistical arbitrage and risk arbitrage, both of which involve risk.
All forms of arbitrage opportunities are based on a buy low, sell high strategy involving the mispriced asset. In competitive markets, pure arbitrage opportunities are expected to be short-lived. Specifically, as arbitrageurs exploit these opportunities, their actions help correct prices, contributing to market efficiency.
In the rest of this lesson, we discuss different types of arbitrage in detail, offering practical examples.
Contents
Pure arbitrage
Pure arbitrage involves two assets with identical cash flows trading at different prices such that there is an opportunity to make money with no risk. In this scenario, one of the assets would be mispriced and the other asset could be a portfolio of fairly-priced assets built to mimic the cash flows of the former.
Strictly speaking, for an arbitrage opportunity to be classified as pure arbitrage, the following three conditions have to hold:
- The strategy has no risk.
- Its expected profit is positive.
- It’s self-financing (i.e., no capital required).
Intuitively, this implies a money machine that requires no investment from you and that provides an opportunity to earn profits without any risk.
Let us give a stylized example from bond markets to explain this. For simplicity, let’s assume we’re dealing with highly-rated government bonds so that we can ignore default risk. In Figure 1, we see the cash flows of a coupon bond that is maturing in two years and two zero-coupon bonds where Zero 1 is maturing in one year and Zero 2 in two years. The price of the coupon bond is $1,100, while Zero 1 and Zero 2 are currently trading at $900 and $825, respectively.
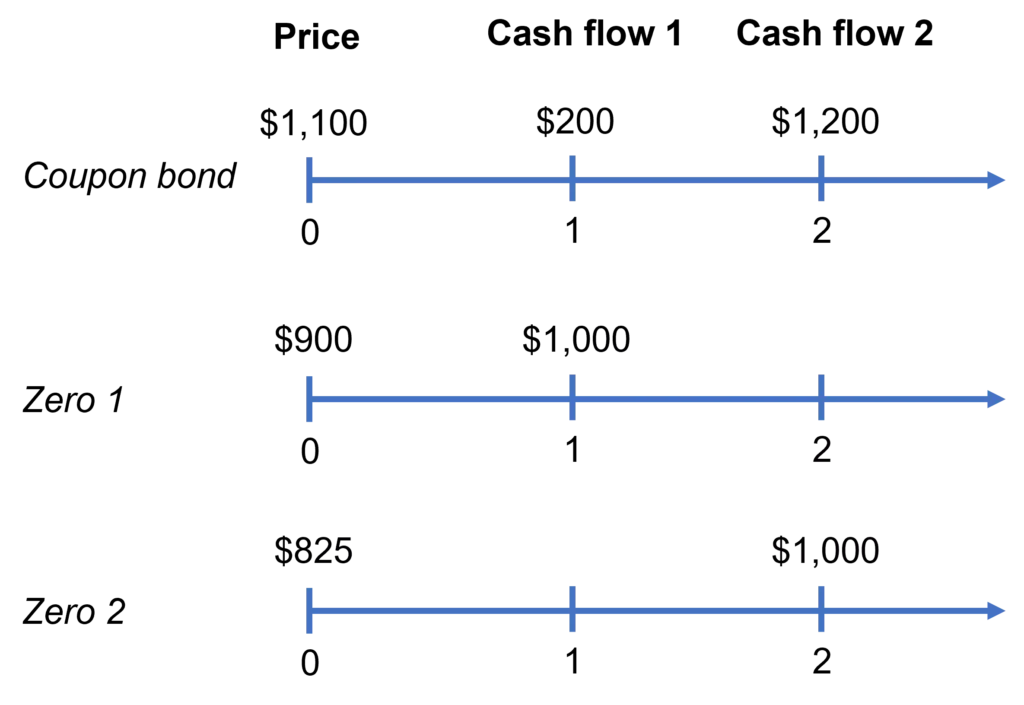
It is easy to see that we can construct a portfolio of Zero 1 and Zero 2 to match the cash flows of the coupon bond. For year 1, to match the coupon bond’s cash flow of $200, we need $200 / $1,000 = 0.2 units of Zero 1. In year 2, the coupon bond is paying $1,200, which means we need $1,200 / $1,00 = 1.2 units of Zero 2. This means that the portfolio that contains 0.2 units of Zero 1 and 1.2 units of Zero 2 would have identical cash flows with the coupon bond. Then, the law of one price requires that:
Price of the coupon bond = 0.2 * Price of Zero 1 + 1.2 * Price of Zero 2
But, we observe that:
$1,100 < 0.2 * $900 + 1.2 * $825 = $1,170
This suggests an arbitrage opportunity, which we can exploit as follows:
- Go short in the portfolio of Zero 1 and Zero 2.
- Use the proceeds raised from the short position to go long in the coupon bond.
Note that this strategy satisfies all of the three conditions stated above. As the cash flows of the coupon bond and the portfolio of zeros are identical, there’s no risk. The short position finances the long position, so no capital is needed. And, the position is guaranteed to generate a profit.
Statistical arbitrage

Statistical arbitrage (also known as StatArb, stat arb, etc.) is a quantitative approach that relies on mean reversion in asset prices to invest in large portfolios for short durations to generate arbitrage profits. The approach requires computational power for implementation. Market risk is usually hedged away by creating portfolios with betas close to zero. In other words, the strategy is market neutral and is meant to work throughout market cycles.
The idea is related to pairs trading, such that the aim is to exploit pricing inefficiencies in highly correlated assets. The technique is popular among hedge funds and investment banks.
Unlike pure arbitrage, statistical arbitrage is risky. It’s based on the premise that the mean reversion that is expected will indeed take place. However, there is uncertainty over how long that would take to happen.
Risk arbitrage (a.k.a. merger arbitrage)

Risk arbitrage is a specific form of arbitrage strategy that focuses on the valuations of acquirers and targets in M&A transactions. For this reason, it is also known as merger arbitrage.
In an M&A deal, an acquirer (or bidder) makes an offer to acquire a target. Typically, this involves a takeover premium. That is, the acquirer offers to pay target shareholders a price that is higher than the target’s current share price.
For example, when HP ($HPQ) announced its intention to acquire Compaq back in 2001, its initial offer valued the target’s shares at a premium of 19% approximately. However, following the announcement, Compaq shares were trading roughly $1 below the price implied by HP’s offer.
The $1 difference between Compaq’s current share price and the price offered by HP is called the merger-arbitrage spread. Investors could exploit this difference by going long in Compaq shares and short selling HP shares.
However, the merger-arbitrage spread doesn’t necessarily imply mispricing because any profit is conditional on the completion of the deal, which is not guaranteed. It isn’t uncommon for merger deals to fall through for a variety of reasons. In fact, the merger-arbitrage spread fluctuates over time, getting tighter/wider as the probability of completion goes up/down.
In the case of HP-Compaq, the merger-arbitrage spread got significantly wider when Walter Hewlett (son of HP co-founder William Hewlett and a company board member) announced his opposition to the deal. If the deal was withdrawn at that point, risk arbitrageurs would face large losses. Luckily for them, things turned around and the deal was eventually completed.
Therefore, like statistical arbitrage, we can’t consider risk arbitrage to be a risk-free strategy.
Video summary
Summary
In this lesson, we explained that the mispricing of an asset creates an arbitrage opportunity in financial markets. A pure arbitrage opportunity carries no risk, whereas risk is involved in both statistical arbitrage, which involves algorithmic trading, and risk arbitrage, which focuses on M&A deals.
Further reading:
Mitchell and Pulvino (2001), “Characteristics of Risk and Return in Risk Arbitrage“, Journal of Finance, Vol. 56(6), pp. 2135-2175.
what is next?
This lesson is part of our course on fundamentals of trading.
- Next lesson: We will move on to a discussion of liquidity, which is a central concept in trading.
- Previous lesson: We discussed the key features of a limit order book.
We hope you enjoyed reading this post, in which case feel free to share it. You can leave us a comment if you noticed any errors or have any suggestions/questions.

