Geometric average return calculator and formula

In this post, we explain the geometric average return formula using numerical examples and discuss how it differs from the arithmetic average return. We provide a practical geometric average return calculator as well.

Geometric average return formula

The geometric average return formula can be written as follows:

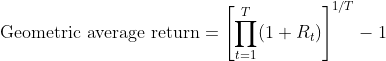
While the formula looks complicated at first sight, it can be easily understood by breaking it down into its elements. First, R_t is the net return in time period t. Then, 1+R_t is the gross return during the same period. T is the total number of periods. Finally, Π is the product symbol, which tells us to compound (i.e., multiply) gross returns over the holding period.

So, to find the geometric mean return over, say, a 12-month period, we need to:

multiply monthly gross returns,
raise the result to the power of 1/12, and
subtract 1.

Let’s illustrate this with an example.

Imagine that you bought a stock a year ago, and the monthly returns over this period were as follows.

Month	Return	Month	Return
January	2.1%	July	−0.2%
February	−1.2%	August	−0.2%
March	−0.6%	September	1.1%
April	0.4%	October	0.4%
May	1.2%	November	−0.1%
June	0.0%	December	1.9%

In this case, calculating the geometric mean return is straightforward. Begin with compounding gross returns:

(1+2.1%) * (1−1.2%) * (1−0.6%) * (1+0.4%) * (1+1.2%) * (1+0.0%) * (1−0.2%) * (1−0.2%) * (1+1.1%) * (1+0.4%) * (1−0.1%) * (1+1.9%) = 1.0485

Raise it to the power of 1/12:

(1.0485)^1/12 = 1.004

And, subtract 1 to get the final result:

1.004 − 1 = 0.004 = 0.4%

Geometric average return calculator

Please note the following when using this calculator:

Enter returns as percentage points. For example, if the first return observation is 20%, simply enter 20 in the “Return 1 (%)” field. If the second return observation is −5%, enter −5 in the “Return 2 (%)” field, and so on.
You can enter up to 10 return observations.
If you have got, say, 3 return observations, make sure to enter them in the Return 1, Return 2, and Return 3 fields, and not in any of the other fields.
The geometric mean return is calculated at the bottom, and the arithmetic mean return is provided for comparison purposes as well.

Geometric average vs arithmetic average

For an investor who held a stock for, say, 24 months, the arithmetic average return simply tells the average of 24 monthly return observations. In contrast, the geometric average return tells about the monthly rate of return at which the investor’s investment grew over the 24-month period.

To illustrate the difference between the two metrics, imagine that you buy a stock for $10, and its value doubles to $20 in the first month, which implies a net return of $20/$10 − 1 = 100%. But, the value of the stock rolls back to $10 in the second month, which is a net return of $10/$20 − 1 = −50%. Note that your holding period return after two months is 0% since you bought the stock for $10 and it’s still worth $10.

Let’s see how the geometric mean return compares with the arithmetic mean return in this case. We can calculate the geometric mean as:

[(1+100%)(1−50%)]^1/2 − 1 = 0%

While the arithmetic mean is:

(100% + (−50%)) / 2 = 25%

So, the geometric mean does a better job of reflecting the investor’s experience over the holding period.

Finally, for any given series of return observations, the geometric mean return is always smaller than the arithmetic mean return. This is because of the mathematics involved in their calculations.

Video summary

Summary

When investors analyze the past performance of their investments, one of the key metrics they focus on is the geometric average (or mean) return. We can calculate it by compounding gross returns and, then, raising that to the power of 1/T where T is the total number of periods (days, months, etc.) involved.

What is next?

If you have enjoyed reading this post, we recommend you check out our free course on investments.

Next lesson: We will introduce the concept of return volatility as a measure of risk.
Previous lesson: We discussed the arithmetic average return as the most basic metric for measuring average investment performance.

For any comments or questions, you can reach us here.

Tags:

return calculations stocks