In this lesson, we introduce a simple yet really useful measure of investment performance. In particular, we discuss the arithmetic average return formula and provide a practical arithmetic average return calculator.
It is really important for investors to be able to accurately assess the performance of their investments. In that sense, arithmetic average (or mean) return proves to be a powerful metric.
Jump to:
Arithmetic average return formula
We can express the arithmetic average return formula as follows:
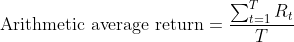
So, the arithmetic average (or mean) return is just a simple average of the return observations. Specifically, Rt represents the net return during the tth period (day, month, year, etc.), and the total number of periods is denoted by T.
To make the formula clearer, consider the following example. Jane bought a stock five years ago. Over this period, the stock generated the returns shown in the table below. Jane wishes to get some sense of the average performance of this stock. But, she doesn’t know how to calculate the arithmetic average return. Let’s help her out.
| Year | Return |
| year 1 | 10% |
| year 2 | 6% |
| year 3 | −4% |
| year 4 | 8% |
| year 5 | 8% |
As per the formula, what we need to do is to find the average of these return observations:
(10% + 6% − 4% + 8% + 8%) / 5 = 5.6%.
So, the arithmetic mean return over this five-year period is 5.6%.
EXERCISE (scroll down to the bottom of the page for the solution): Robin wants to evaluate the performance of a stock he bought four months ago. In January, the stock performed well, yielding a return of 5%. There was not much movement in the stock price in February, and the return was 0.2%. The stock price fell in both March and April, yielding returns of −1% and −0.6%, respectively. Help Robin calculate the arithmetic average return.
Arithmetic average return calculator
When using the arithmetic average return calculator below, please bear in mind the following:
- You can enter as many as 12 return observations (or as few as 1).
- If you need to enter, say, 4 return observations, use the following fields: Return 1, Return 2, Return 3, and Return 4. The calculator would not work properly if you jumped to other fields.
- Enter data as percentage points (e.g., enter 10 if the return is 10%).
summary
At the start of our investments course, we covered basic return calculations and discussed fundamental concepts such as real returns vs nominal returns.
With this lesson, we have moved on to the topic of popular measures investors use to compute average realized (or historical) returns. To this end, we have presented the arithmetic average return formula and have provided an arithmetic average return calculator.
Further reading
Missiakoulis et al. (2010) ‘Arithmetic mean: a bellwether for unbiased forecasting of portfolio performance‘ Managerial finance, Vol. 36 (11), pp. 958-968.
what is next?
This lesson is part of our online course on investments, which covers topics ranging from portfolio theory to asset pricing models such as the capital asset pricing model.
- Next lesson: In the next lesson, we will be introducing another popular measure for calculating average returns: geometric average return.
- Previous lesson: We explained how to make holding period return calculations.
EXERCISE SOLUTION: In this case, we have the following four monthly return observations: 5%, 0.2%, −1%, and −0.6%. Then, using the arithmetic average return formula, we have (5% + 0.2% − 1% − 0.6%) / 4 = 0.9%. You can verify this answer using the arithmetic average return calculator given above. Simply enter 5, 0.2, −1, and −0.6 in the first four fields.
