We often say that risk and return are two sides of the same coin. So, when assessing the performance of a portfolio, we need to consider its risk as well as its return. In the previous lesson, we focused on portfolio return. Now, we turn our attention to portfolio risk.
Contents
Portfolio risk calculator
You can use the portfolio risk calculator below for portfolios containing up to three assets. Please note the following instructions:
- For Asset 1, enter its variance (σ12) and its covariances with Asset 2 (σ12) and Asset 3 (σ13).
- For Asset 2, enter its variance (σ22) and its covariance with Asset 3 (σ23).
- Finally, for Asset 3, enter its variance (σ32) only.
- If your portfolio consists of 2 assets only, just leave 0s in the fields that you don’t need.
- Make sure that investment weights add up to 100% (see the “sum of weights (%)” in the last row).
- The calculator allows for both positive investment weights and negative investment weights (i.e., short selling).
Portfolio risk formula
In the previous lesson, we explained that a portfolio’s return is simply a weighted average of the returns of assets that constitute the portfolio. And, the weights are determined by the amount invested in each asset. This led us to the formula for portfolio return RP:
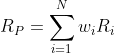
where wi is the investment weight for asset i and Ri is the realized return for asset i. In an earlier lesson, we introduced the variance of returns (let’s denote that as σi2 for asset i) as a measure of risk. Could we then calculate the variance of returns on a portfolio σP2 as a weighted average of the variance of assets in that portfolio? In other words, would the following equation capture portfolio risk?
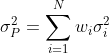
The answer is no. When calculating σP2, we need to consider not only the variance of each asset but also the covariance between each pair of assets. To understand why, imagine a portfolio with two assets only. Suppose that when the price of one asset goes up, the price of the other tends to go down. These opposite movements would partially cancel out each other, reducing the volatility of portfolio returns. So, the portfolio risk formula is:
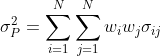
where wi is the investment weight for asset i, wj is the investment weight for asset j, and σij is the covariance between assets i and j.
It is worth noting that the covariance between two assets σij can be computed using the correlation coefficient between the same two assets ρij as follows:

Portfolio variance with two assets
For a portfolio containing two assets (A and B), the general portfolio risk formula simplifies into:
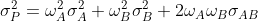
So, in a two-asset portfolio, σP2 depends on:
- The variance of returns for each asset (σA2 and σB2).
- The covariance between the returns of asset A and asset B (σAB).
- And, the investment weights (wA and wB).
Portfolio variance with three assets
If a third asset (C) is added to the portfolio, we have:
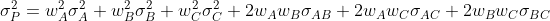
Then, in a three-asset portfolio, σP2 depends on:
- The variance of returns for each asset (σA2, σB2, and σC2).
- The covariance between each pair of assets (σAB, σAC, and σBC).
- And, the investment weights (wA, wB, and wC).
Portfolio variance with N assets
If we kept adding assets to the portfolio, we’d end up with the following formula:
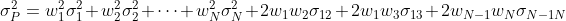
This means that for a portfolio of any size, portfolio risk depends on the individual risk of each asset in the portfolio (σ12, σ22, …, σN2), the covariance terms (σ12, σ13, …, σN-1 N) and investment weights (w1, w2, …, wN).
Test your knowledge
Gareth holds a portfolio of three stocks as shown in the table below. The correlation between stocks A and B is −0.44. Stock C is uncorrelated with the other two stocks. Can you help Gareth compute the variance and standard deviation of his portfolio returns?
Note: You can use the portfolio risk calculator above, and the solution is provided at the bottom of this page.
| Stock | Investment | Risk (standard deviation of returns) |
|---|---|---|
| A | $200 | 30% |
| B | $800 | 10% |
| C | $1,000 | 40% |
Summary
In this lesson, we have explained the portfolio risk formula, highlighting the importance of covariances between asset pairs. We have also provided a handy portfolio risk calculator.
Further reading:
Markowitz (1991), “Foundations of Portfolio Theory“, The Journal of Finance, Vol. 46 (2), pp. 469-477.
What is next?
This lesson is part of our free course on investments.
- Next lesson: We’ll investigate how investors can conduct mean-variance optimization to construct portfolios that are efficient in terms of risk and return.
- Previous lesson: We explained how to calculate portfolio returns.
Solutions for the “test your knowledge” exercise
Let’s first compute the investment weights. The total investment is:
$200 + $800 + $1,000 = $2,000
Then, the investment weights are:
wA = $200 / $2,000 = 10%, wB = $800 / $2,000 = 40%, wC = $1,000 / $2,000 = 50%
The variances of each stock are:
σA2 = (30%)2 = 0.09, σB2 = (10%)2 = 0.01, σC2 = (40%)2 = 0.16
The covariance between stock A and stock B is:
σAB = ρAB * σA * σB = −0.44 * 30% * 10% = −0.0132
Because stock C isn’t correlated with the other stocks, we have:
σAC = 0 and σBC = 0
Finally, we can use the portfolio risk calculator above to get the result as follows:

This means that the standard deviation of returns for this portfolio is 0.2035, or 20.35%.
Of course, using the portfolio risk formula for three assets would give the same result:
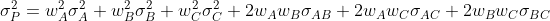
σP2 = (10%)2(30%)2 + (40%)2(10%)2 + (50%)2(40%)2 + 2(10%)(40%)(−0.0132) + 0 + 0 = 0.0414
and σP = 0.2035 = 20.35%.

