In this post, we explain the formula behind the calculation of portfolio returns. Furthermore, we provide a free online portfolio return calculator, which works as a portfolio expected return calculator as well as a portfolio realized return calculator. Finally, with this port, we make an introduction to the modern portfolio theory as well.
So far in this course on investments, we have focused on investing in a single asset. However, in reality, many investors invest in more than one asset and hold portfolios of assets. Furthermore, there is a massive investment management industry out there, including mutual funds, exchange-traded funds, hedge funds, insurance funds, pension funds, sovereign wealth funds, and so on. In essence, these investment companies are portfolios that are run by professional portfolio managers. Therefore, for anyone interested in finance and investing, it is important to be able to calculate portfolio returns.
Learning objectives
- Understand the concept of investment weight.
- Learn how to calculate the return on a portfolio of assets.
Jump to:
Investment weights
Imagine that you have $5,000 to invest. If you invest all that amount in a single asset, say Pfizer shares, the return on your investment will solely depend on the performance of Pfizer shares.
However, if you split your investment such that you invest $4,000 in Pfizer shares and $1,000 in Procter & Gamble shares, then the performance of your portfolio will depend on the performance of Procter & Gamble shares as well as Pfizer shares. In this scenario, you invest $4,000 / $5,000 = 80% of your funds in Pfizer. And, the remaining $1,000 / $5,000 = 20% in Procter & Gamble. In other words, your investment weights (or portfolio weights) for Pfizer and Procter & Gamble are 80% and 20%, respectively. Given that the investment weight of Pfizer is much bigger than that of Procter & Gamble, the performance of your portfolio will be more heavily influenced by Pfizer shares.
Portfolio return formula
If the returns of Pfizer and Procter & Gamble last month were 2% and −1%, respectively, then your portfolio return would simply be the weighted average of these returns:
80% (2%) + 20% (−1%) = 1.4%
Let’s go further and add a third stock to your portfolio: Nike, such that you invest $3,000 in Pfizer, $1,000 in Procter & Gamble, and $1,000 in Nike. Note that the total investment is still $5,000. Now, the updated investment weights are 60% for Pfizer, 20% for Procter & Gamble, and 20% for Nike (this is also referred to as your portfolio composition). If Nike’s return last month was 0.5%, your portfolio return would become:
60% (2%) + 20% (−1%) + 20% (0.5%) = 1.1%
In general, the realized (or historical) return on a portfolio RP can be calculated as:
RP = ∑wi Ri
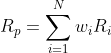
where wi is the investment weight for asset i and Ri is the realized return for asset i.
How about the portfolio expected return E[RP]? The idea is still the same. In fact, we can simply replace the realized return of each asset in the portfolio with its expected return:
E[RP] = ∑wi E[Ri]
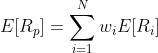
For example, if the expected returns of Pfizer, Procter & Gamble, and Nike for the next month are 1.4%. 2%, and 0.9%, respectively, then your portfolio’s expected return is:
60% (1.4%) + 20% (2%) + 20% (0.9%) = 1.42%
In summary, the return of a portfolio depends on (a) the return of each asset within that portfolio and (b) the investments weights for those assets, such that assets with larger investment weights influence the portfolio return more than those with smaller investment weights.
Portfolio return calculator
Instructions
You can use the portfolio return calculator below to calculate the return on a portfolio of up to 5 assets. It can be used as a portfolio expected return calculator or a portfolio realized return calculator. Please note the following instructions:
- The calculator allows for both positive investment weights and negative investment weights (i.e., short selling).
- Make sure that investment weights add up to 100% (see the “sum of weights (%)” in the last row of the calculator).
- Make sure to enter data as percentage points. For example, if the investment weight is 80%, simply enter 80 in the “weight (%)” field, and if the return is -5%, just enter -5 in the “return (%)” field.
- If your portfolio consists of less than 5 assets, you can of course use the calculator by leaving 0s in the fields that you don’t need.
Calculator
Summary
If you are spreading your funds across several assets, which is typically a good idea, you need to be able to calculate portfolio returns. In this post, we show that the return on a portfolio can be calculated as a weighted average of returns on assets included in that portfolio. And, the weights are proportional to the amounts you invest in those assets. Finally, we offer a portfolio return calculator that functions as both a portfolio expected return calculator (i.e., forward-looking) and a portfolio historical return calculator (i.e., backward-looking).
Further reading:
If you would like to learn more about the historical development of modern portfolio theory, we recommend the following article.
Markowitz (1999), ‘The Early History of Portfolio Theory: 1600–1960,’ Financial Analysts Journal, Vol. 55 (4), pp. 5-16.
What is next?
This post is part of our free course on investments. Now that we have learned how to calculate portfolio return, we will discuss how to calculate portfolio risk in the next post. The subject of the previous post was the concept of risk premium.
We very much hope that you found this post useful. If so, please consider sharing it with others whom you think may find it useful as well. Also, if you happen to have any questions or suggestions, you are welcome to leave a comment below.
