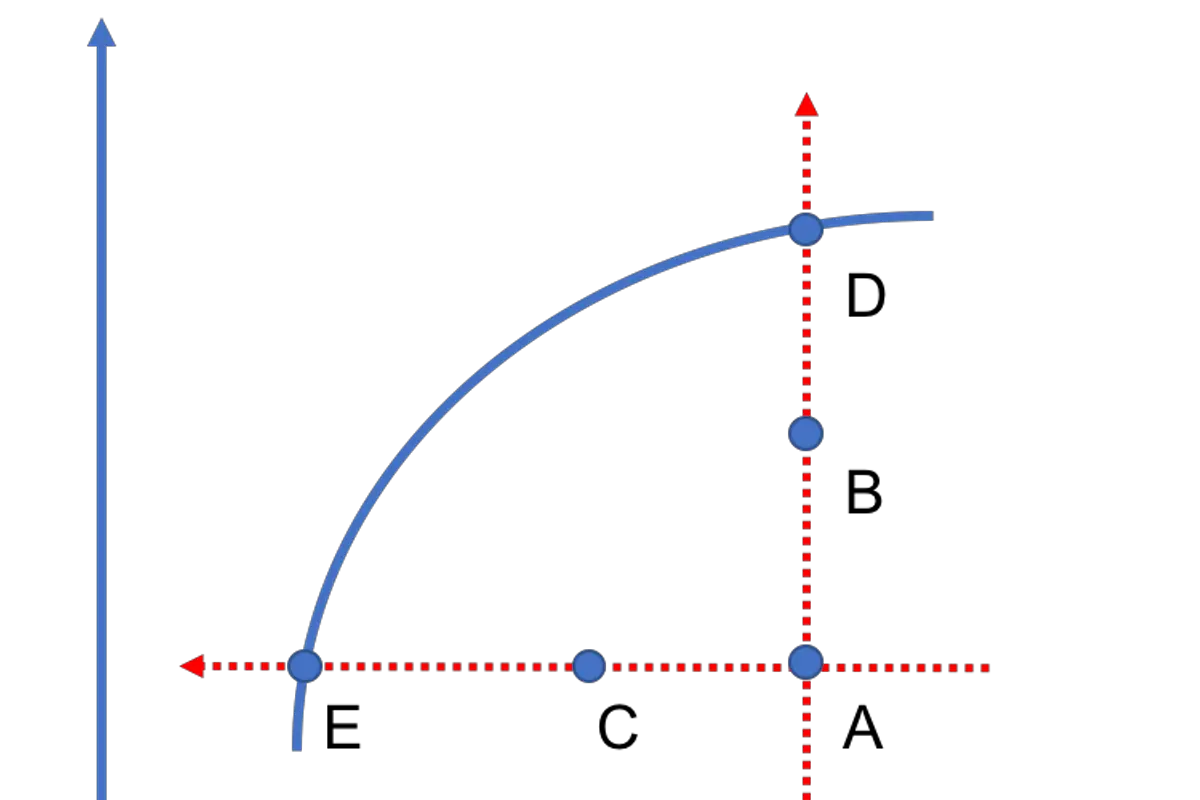
In modern portfolio theory, the efficient frontier represents the collection of all efficient portfolios within a market. Efficient portfolios offer the best risk-return tradeoff and, as such, are superior to inefficient portfolios, which are suboptimal.
In this lesson, we explain how investors can trace the efficient frontier using mean-variance optimization (the topic of the previous lesson) and how Excel can be used as an efficient frontier calculator.
Contents
Tracing the efficient frontier
As we have discussed in the previous lesson on mean-variance optimization, investors should seek the portfolio with the highest return among portfolios that have the same level of risk. And, they should search for the portfolio that bears the least risk among portfolios that offer the same return. We further examine this strategy in Figure 1.
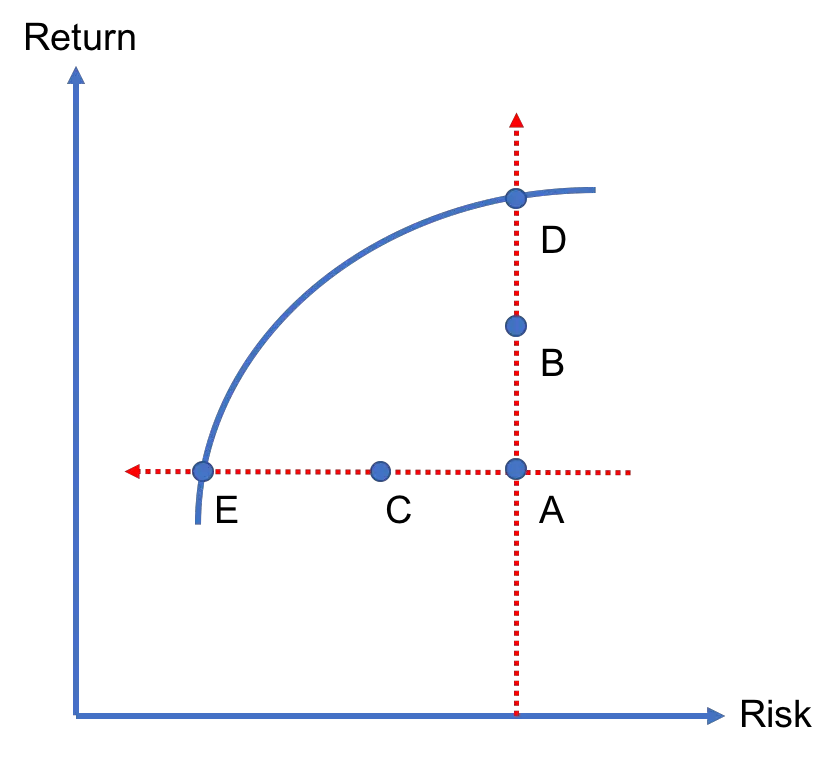
Portfolios A, B, and D have the same level of risk. Among these portfolios, investors would choose D as it has the highest return. If there are no other portfolios that offer a higher return than D for the same level of risk, then D is an efficient portfolio.
Furthermore, portfolios A, C, and E offer the same level of return. Among them, portfolio E carries the least amount of risk. So, investors would prefer E over A and C. We consider E an efficient portfolio if there is no other portfolio that has less risk for the same amount of return.
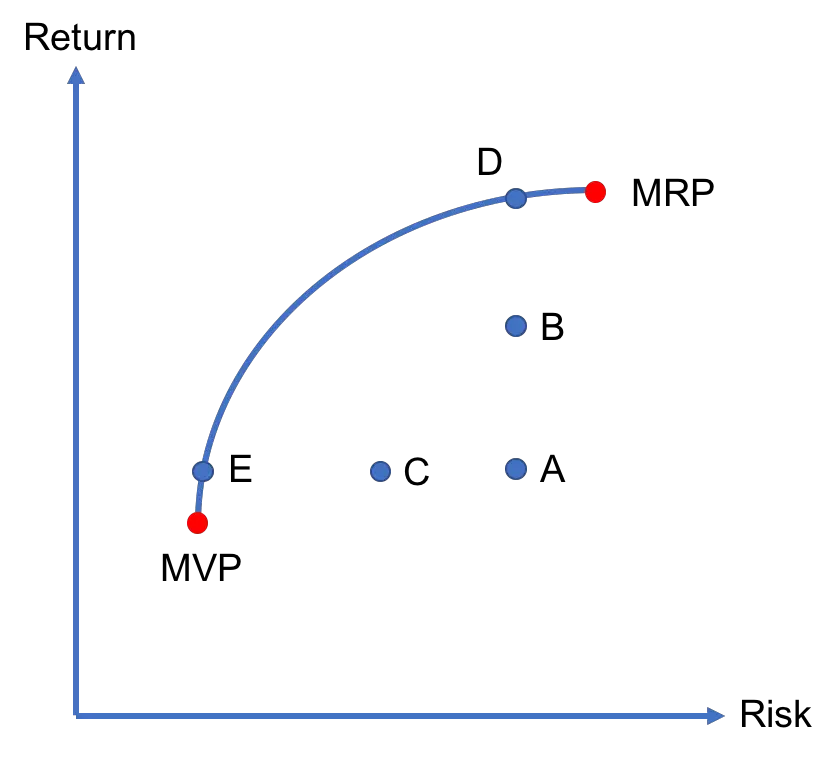
In summary, both D and E are efficient portfolios. If we connect all efficient portfolios (D, E, and others), we end up with the efficient frontier. Portfolios that are not part of the efficient frontier are inefficient (see Figure 2). Investors should avoid them as for any inefficient portfolio (say A), they can find an efficient portfolio that offers either more return (D) or less risk (E).
How about choosing between D and E? This very much depends on the investor’s degree of risk aversion. An investor who is very risk averse would likely choose E over D, whereas another who is willing to bear more risk might invest in D or another nearby efficient portfolio. The good news is that when there is a risk-free asset in the economy, there is a single optimal risky portfolio as we discuss later in the course.
Using Excel as an efficient frontier calculator
It is possible to use Excel as an efficient frontier calculator thanks to the Solver add-in. Here are the steps to follow (referring to Figure 3 below where appropriate):
- Determine the expected return and variance for each asset and also the covariance between each pair of assets. For example, stock A’s expected return is 3, variance is 10, and covariance with B is 1.
- Enter initial values for the investment weights (cells I4 to I7). You can choose random values.
- Compute the return (cell E9) and risk (cell E10) of the portfolio based on the initial weights.
- Compute the sum of investment weights (cell E11).
- Click on Solver and set the objective to minimize (Min) the portfolio risk (cell E10),
- By changing investment weights (I4 to I7),
- Subject to investment weights adding up to one (E11 = 1),
- And set the portfolio return at a fixed level (here we begin with E9 = 4, and later the portfolio return is set to 6, 8, and 10 as well – notice the orange data points).
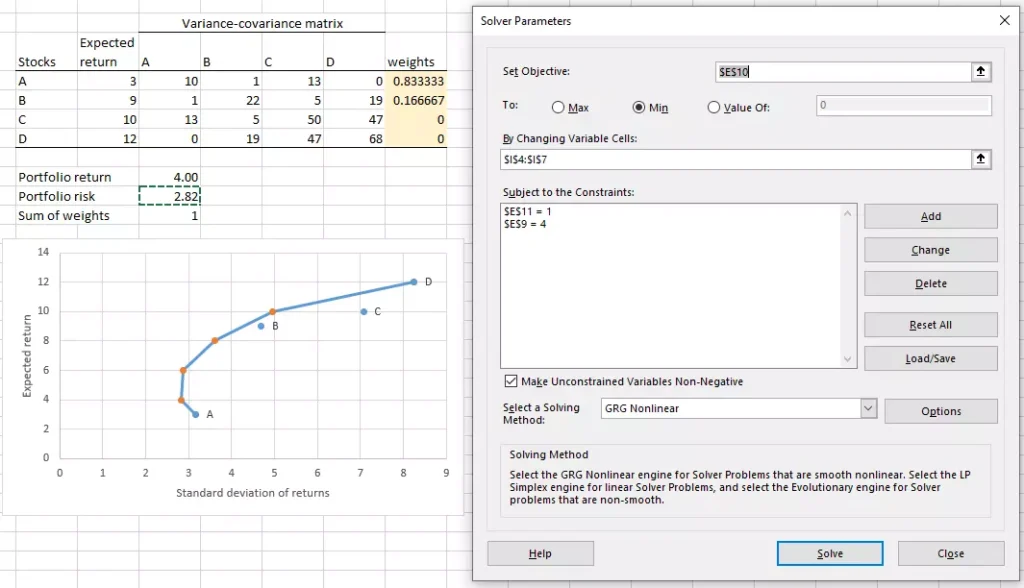
Looking at Figure 3 above, we observe that the efficient portfolio with an expected return of 4 (see the first orange data point to the left of stock A) invests 83.33% in A and 16.67% in B (see the yellow cells). Furthermore, the same efficient portfolio is preferable to stock A as it offers more return (4 vs 3) for less risk (2.82 vs √10=3.16).
If you would like to allow for short selling in the market, in the Solver dialog box, uncheck the box where it says “Make Unconstrained Variables Non-Negative”.
It is common to have convergence problems with Solver, particularly when you have an unusual variance-covariance matrix. So, don’t be discouraged by that. You can try different initial values and solving methods or review your input estimates to resolve such issues. Good luck with your analysis!
Video tutorial and Excel template
Here you can find our video tutorial on tracing the efficient frontier in Excel. You can also download the Excel spreadsheet we use in the tutorial.
Summary
At the heart of the modern portfolio theory developed by Harry Markowitz lies the idea that investors care about the mean and variance of potential returns of investment opportunities. Making optimal choices under this framework leads to an efficient frontier, which offers the best “deals” in capital markets. Tools such as Excel’s Solver can work as an efficient frontier calculator.
Further reading:
Elton et al. (1978), “Simple Criteria for Optimal Portfolio Selection: Tracing Out the Efficient Frontier“, The Journal of Finance, Vol. 33(1), pp. 296-302.
What is next?
This lesson is part of our free course on investments.
- Next lesson: We will be discussing the minimum variance portfolio, which is the leftmost portfolio on the efficient frontier in the absence of a risk-free asset.
- Previous lesson: We have focused on mean-variance optimization and how that aids portfolio selection for investors.
If there is anything we can do to make our content more useful for you, let us know by writing to us.