According to modern portfolio theory, investors are concerned about the “mean” and “variance” of asset returns, where the former captures the “centrality” and the latter the “spread” (or “riskiness”) of potential returns. As such, investors engage in mean-variance optimization. That is, they seek the portfolios that offer the best tradeoff between risk and return.
In the remaining part of this lesson, we explain how investors can choose among portfolios through mean-variance optimization, using the two-asset case as an illustrative example.
Contents
Portfolio choice through mean-variance optimization
Not all portfolios of assets are equally good. Some are better than others. Therefore, it is important for investors to place their funds in the best portfolios that can be constructed in a market. They should avoid investing in suboptimal portfolios.
But, how can investors tell apart good portfolios from bad ones? To answer that question, we need a method to compare portfolios. The method we will use is mean-variance optimization, which compares portfolios in terms of their return and risk. That is, the “mean” captures return and the “variance” reflects risk.
Furthermore, we will rely on two reasonable assumptions:
- Investors prefer more return to less return.
- Investors prefer less risk to more risk.
The first assumption is based on investors’ insatiable appetite for higher returns: If portfolios A and B have the same level of risk, and if B offers a higher return than A, all investors would prefer B to A. The second assumption is related to investors’ aversion toward risk: That is, if portfolios A and C have the same level of return, but C is less risky than A, investors would choose C over A.
We illustrate these choices in Figure 1. Investors prefer B over A because of an insatiable appetite for higher returns. Moreover, they prefer C over A because of their general dislike for risk. Therefore, portfolio A is inefficient compared to portfolios B and C. As a result, rational investors should avoid investing in portfolio A. It is dominated by portfolios B and C.
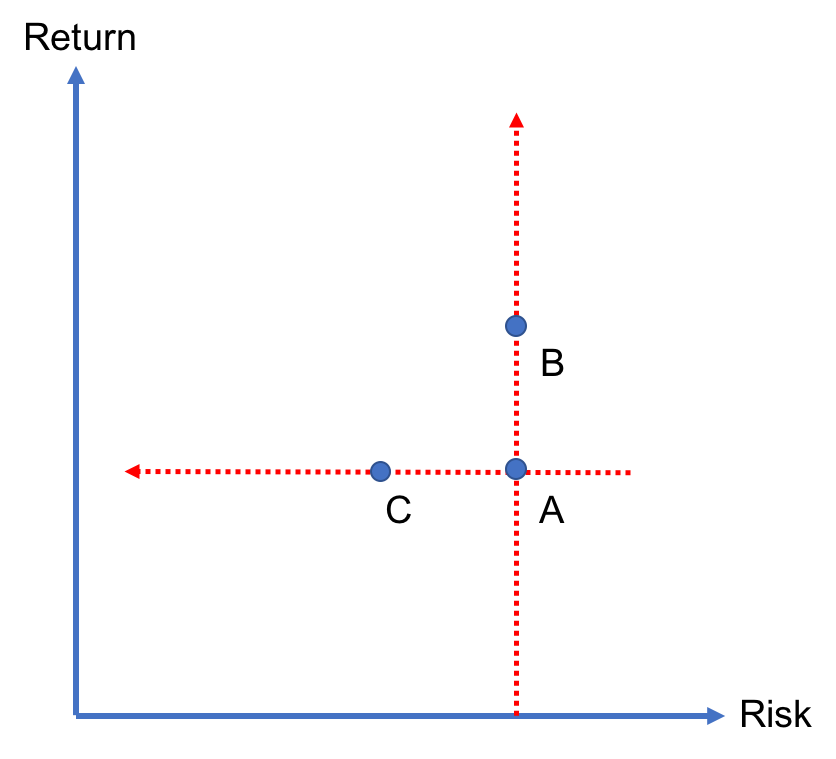
Overall, mean-variance optimization is the pursuit of the portfolio that has the highest return for a given level of risk (or the lowest risk for a given level of return). It leads to what is known as the efficient frontier as we discuss in the next lesson.
Mean-variance optimization with two assets
In Figure 2, we observe two individual assets: stock A and stock B, and combinations of these two stocks in a portfolio, which is depicted by the blue curve that extends from A to B. For example, C represents a portfolio that invests 60% in A and 40% in B.
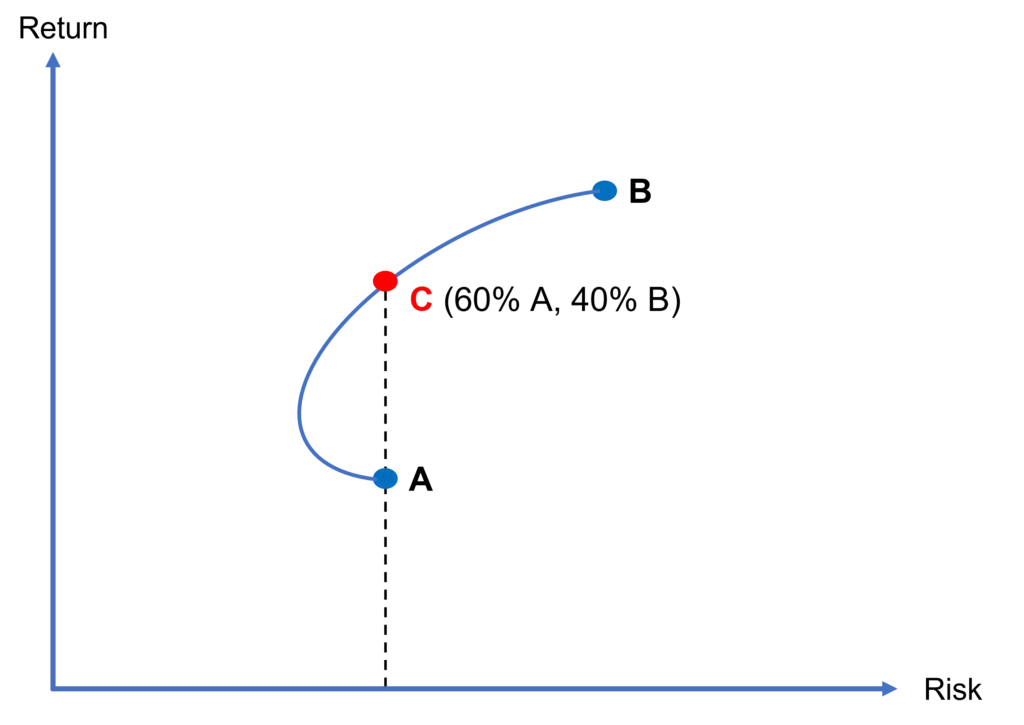
We also observe that C has the same level of risk as A but offers a substantially higher return than A. So, mean-variance optimization dictates that an investor should prefer investing in C (a portfolio of A and B) over investing in A alone. In other words, it would be irrational to hold A only.
How about the choice between B and C? This depends on the investor’s degree of risk aversion. Theoretically, the investor would choose one of the efficient combinations of A and B that maximizes her utility. More on that in our next lesson.
Video summary
Summary
In this lesson, we have explained how investors can choose between various investment opportunities based on mean-variance optimization. In particular, investors would seek the highest possible return for a given level of risk and the lowest possible risk for a given level of return. This would lead them to identify portfolios that offer the best risk-return tradeoff in the market.
Further reading:
Björk et al. (2014) “Mean-variance portfolio optimization with state‐dependent risk aversion“, Mathematical Finance, Vol. 24(1), pp. 1-24.
What is next?
This lesson is part of our free course on investments.
- Next lesson: We will discuss how an efficient frontier emerges as investors engage in portfolio optimization.
- Previous lesson: We explained how to calculate portfolio risk, which involves covariances as well as variances of the assets within the portfolio.
We would love to hear back from you. If you have got any feedback on our content, feel free to get in touch.

