When we discussed investors’ risk preferences, we distinguished between risk-averse, risk-neutral, and risk-seeking behavior. We also explained that risk-averse investors expect compensation for bearing risk, which is called a risk premium. But, how do measure a person’s level of risk aversion? The answer is the risk aversion coefficient. It quantifies the degree to which an individual dislikes risk.
In this lesson, we introduce the formulas of Arrow-Pratt coefficients of absolute risk aversion and relative risk aversion. We discuss how economists estimate risk aversion coefficients and the typical range of coefficient estimates.
Contents
Absolute risk aversion coefficient
The Arrow-Pratt absolute risk aversion coefficient (ARA) tells us an individual’s degree of risk aversion at a particular level of wealth, hence the adjective “absolute”. Intuitively, a $10,000 gamble would mean different things to the “rich” versus the “poor”. In particular, a wealthy CEO can be expected to be much less averse to such a gamble than, say, a blue-collar worker. For that reason, absolute risk aversion decreases with the level of wealth.
The Arrow-Pratt absolute risk aversion coefficient is calculated by dividing the second derivative of the utility function u”(w) by its first derivative u'(w) as shown below.
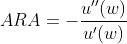
Note that the negative sign is used to obtain a positive value for ARA as the second derivative of the utility function is negative (u”(w)<0).
Example 1
Let’s assume that an individual has a power utility function as follows:
u(w) = −w−1
In this case, the first and second derivatives of u(w) are as follows: u'(w) = w−2 and u”(w) = −2w−3. Then, this individual’s absolute risk aversion coefficient is:
ARA = − (−2w−3) / (w−2) = 2 / w
Notice that the individual has decreasing absolute risk aversion: ARA gets smaller as w gets larger.
Relative risk aversion coefficient
The Arrow-Pratt relative risk aversion coefficient (RRA) aims to capture the degree of risk aversion given a proportional change in wealth (e.g., a 5% increase in wealth). As such, it is closely related to the absolute risk aversion coefficient and can be calculated by multiplying ARA by the level of wealth w as follows:
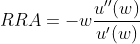
Constant relative risk aversion would imply that an individual has the same degree of aversion to, say, a 10% change in wealth, regardless of how rich or poor that person is.
Example 2
In the previous example, we showed that when the utility function for an individual is u(w) = −w−1, that individual has ARA = 2 / w. Then, the RRA for the same individual is:
RRA = w ARA = w (2 / w) = 2
This means that the individual exhibits constant relative risk aversion as her RRA is always equal to 2 regardless of the leverl of her wealth.
Measuring risk aversion and typical estimates
Economists use various methods to estimate risk aversion coefficients. For example, an early study by Friend and Blume (1975) (see the full reference at the end) relies on cross-sectional survey data on household asset holdings. They find that the RRA coefficient is “well in excess of one and probably in excess of two” (p. 900).
Another common approach to measuring risk aversion is based on a consumption-based CAPM. Adopting such an approach Hansen and Singleton (1983) find that the coefficient of relative risk aversion lies between 0 and 2.
More recently, Chetty (2006) uses data on labor supply behavior to measure risk aversion. He argues that based on existing evidence of the effects of wage changes on labor supply, the RRA coefficient should be less than 2.
A review paper by Gándelman and Hernández-Murillo (2015) (full reference at the end) notes a wide range from 0.2 to 10 or higher. However, they add that “the most widely accepted measures lie between 1 and 3” (p. 53). According to their analysis, the coefficient of relative risk aversion varies closely around the value of 1 across the 75 countries in their sample.
Summary
In this lesson, we have explained the meaning of “risk aversion coefficient” and have distinguished between Arrow-Pratt measures of absolute risk aversion and relative risk aversion. After that, we discussed how economists measure risk aversion in practice. We wrapped our discussion by pointing out that relative risk aversion coefficient estimates range from 0.2 to 10 or higher across studies with estimates between 1 and 3 generally accepted as the most typical.
Further reading
Chetty (2006) “A New Method of Estimating Risk Aversion” The American Economic Review, Vol. 96 (5), pp. 1821-1834.
Friend and Blume (1975) “The demand for risky assets” The American Economic Review, Vol. 65 (5), pp. 900-922.
Hansen and Singleton (1983) “Stochastic Consumption, Risk Aversion, and the Temporal Behavior of Asset Returns” Journal of Political Economy, Vol. 91 (2), pp. 249-265.
Gándelman and Hernández-Murillo (2015) “Risk aversion at the country level” Federal Reserve Bank of St. Louis Review, First Quarter 2015, 97(1), pp. 53-66.
What is next?
This post is part of our free course on investments.
- Next lesson: We elaborate on an important implication of risk aversion: risk premium.
- Previous lesson: We explained different attitudes toward risk: risk aversion, risk neutral, and risk seeking.
If you liked this post, feel free to share it within your network. And, if anything is unclear or if you’ve got any suggestions, you can leave us a comment here.

