Contents
Risk premium definition
The risk premium for a security (e.g., stock, bond, etc.) can be defined as the return the security generates over the risk-free rate of return. For example, if the yields on government bonds are 3%, and a stock is expected to return 8%, then this stock’s risk premium is 8% − 3% = 5%.
More generally, if the expected return on a risky asset is E[R] and the risk-free rate is Rf, then the risk premium formula is:
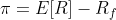
For ease of interpretation, we can rewrite this formula as follows:
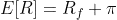
It tells us that a risky asset’s expected return is equal to the risk-free rate PLUS a risk premium. It implies that we would invest in a risky asset only if it offers a return higher than the risk-free rate. This is a direct consequence of investors’ aversion to risk: Risk-averse investors would bear risk only if they are rewarded for doing so. And, the risk premium is the reward they receive.
In general, the riskier the asset, the higher the risk premium should be. So, if asset A is riskier than asset B, we have:
πA > πB
If that is the case, we can deduce that asset A’s expected return, which is E[RA] = Rf + πA, should be higher than asset B’s expected return, which is E[RB] = Rf + πB:
E[RA] > E[RB] since πA > πB
Risk premium calculator

To use the risk premium calculator below, enter (i) the asset’s return, and (ii) the return on the risk-free asset. You might find our CAPM calculator useful as well.
Video summary
Summary
An asset’s risk premium captures the additional return the asset is expected to generate over a risk-free asset such as government bonds. Risk-averse investors wouldn’t invest in risky assets such as stocks in the absence of a sufficient premium.
Further reading:
Chan et al. (1992), ‘Global financial markets and the risk premium on U.S. equity‘ Journal of Financial Economics, Vol. 32(2), pp. 137-167.
What is next?
This lesson is part of our free course on investments.
- Next lesson: We will be moving on to the topic of portfolio theory and will begin with teaching how to calculate portfolio returns.
- Previous lesson: We introduced the risk aversion coefficient as a means for quantifying an individual’s degree of risk aversion.
We hope you like our content and would be happy to hear from you if you have any feedback for us. You can reach us here.

