The risk-free rate is the rate of return earned on a risk-free asset. While returns on risky assets such as stocks are uncertain, the key distinction of the risk-free rate of return is that we know its exact value at the time of investment. For example, we may expect a stock to yield 8% over a year, but the stock’s actual return may be well above or below that. In contrast, if the risk-free rate of return over a year is 3%, we are certain to earn that return by the end of the year.
Contents
Risk-free asset

Many assets we are familiar with don’t fit the profile of a risk-free asset.
Think about stocks. If you invest in, say, Amazon shares today, you might have a target price in mind for the next year. However, the actual price in a year may be very different than what you expected (in a good or bad way). So, there is risk involved.
The same goes for real estate. Suppose you buy a house with the purpose of selling it ten years later. While you’d hope you’ll make a good profit through the future sale, the exact selling price will depend on the market conditions at that time. If the housing market is struggling, you might even face the prospect of selling your property at a loss…
How about corporate bonds? These are debt instruments issued by corporations (e.g., Microsoft, Disney, etc.). Corporate bonds vary in quality (and are graded by credit agencies such as S&P, Moody’s, etc.), and some are pretty safe. But, they all carry default risk to varying degrees, so even the bonds issued by top corporations cannot be considered fully riskless.
Our best candidates for a risk-free asset are government securities such as treasury bills or bonds. “But, governments can also default!” we hear you say. And, you are right. According to the World Economic Forum, more than 100 governments defaulted on their debt since 1960.
However, there are several reasons why government debt is considered a better candidate for being a risk-free asset than other securities: The consequences of a default on sovereign debt are much more severe than a single corporation defaulting on its bonds. The governments would do everything in their power to avoid such a scenario. And, they indeed have powers that other economic agents don’t have. They can raise taxes or even “print” money (quantitative easing!) to fulfill their debt obligations. Of course, these tools need to be used with caution, but they can help governments “save the day” on certain occasions.
How to find the risk-free rate?

Finance students, and even beginner investors/analysts, can sometimes struggle with finding an appropriate risk-free rate to conduct their analyses. As we explained above, using treasury yields is the conventional solution in most practical applications. Still, there are a number of factors to bear in mind:
Data sources:
Treasury yields can be obtained from free financial data providers as well as subscription-based ones. Moreover, it is possible to obtain historical data from both types of sources as well.
For example, Yahoo! finance provides data on 13-week Treasury Bills (^IRX), Treasury Yield 10 Years (^TNX), Treasury Yield 30 Years (^TYX), etc. It is easy to access government yield curves from public sources as well (see. e.g., Financial Times’ bond data section).
Investment horizon:
It’s important that the maturity of the treasury bill/bond you choose matches your investment horizon. In general, treasury bills have maturities up to a year whereas treasury notes and treasury bonds have longer maturities. If your investment horizon is one year, you can take the yield on a 1-year treasury bill (T-bill) as the risk-free rate. But, if it is the next 20 years, then you can focus on the yield on a 20-year treasury bond. The problem with using the 1-year T-bill yield when the investment analysis is for 20 years would be the reinvestment risk. That is, there would be uncertainty about treasury yields once the 1-year T-bill matures with 19 years of the investment horizon remaining.
Risk-free rate formula
Another common query finance students have is whether there is a “formula” for the risk-free rate. Well, the answer depends on what exactly is needed.
For example, sometimes we need to make a distinction between the real versus nominal risk-free rate (if you are unfamiliar with the distinction between real return and nominal returns, you can check our separate lesson on that here). In this case, we can use the following formula:
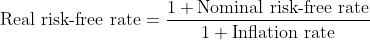
Other times, we may just need to be able to compute the yield of a government bond (based on its price, coupon rate, and face value), so that we can use that as the risk-free rate. As a simple example, if a treasury bill that has a maturity of one year is selling for $900, and if its face value is $1,000, then its yield is $1,000 / $900 − 1 = 11.11%. For treasury bonds, we can use Excel to compute their yield to maturity.
Relationship with CAPM
Later in this course, we will cover the topic of the capital asset pricing model (CAPM), which is extensively used by both practitioners and academics. CAPM suggests a link between the expected return on any asset and its beta (i.e., the asset’s sensitivity to market movements):
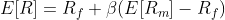
where E[R] is the expected return on the asset, E[Rm] is the expected return on the market portfolio, β is the asset’s beta, and Rf is the risk-free rate of return.
Stocks that have betas that are higher than 1 are sometimes called aggressive stocks as they are highly sensitive to market movements. In contrast, defensive stocks are those with betas less than one.
Using the CAPM equation, we can prove that the beta of the risk-free asset is equal to zero:
E[R] = Rf + β ( E[Rm] − Rf )
As the expected return for the risk-free asset is E[R] = Rf, we have:
Rf = Rf + β ( E[Rm] − Rf )
Rf − Rf = β ( E[Rm] − Rf )
0 = β ( E[Rm] − Rf )
The last equation holds if β=0 (because E[Rm] > Rf).
Summary
The risk-free asset can be described as an asset that has no uncertainty with respect to its return. It has a beta of zero as well as zero volatility.
In practical applications, and particularly in the case of developed markets, yields on government securities can serve as useful estimates of the risk-free rate. It is important to bear in mind the investment horizon when choosing among treasuries, though, so that a reinvestment risk can be avoided.
Further reading:
Weil (1989) ‘The equity premium puzzle and the risk-free rate puzzle‘, Journal of Monetary Economics, Vol. 24(3), pp. 401-421.
What is next?
This lesson is part of our free course on investments.
- Next lesson: We will define what is meant by risk appetite and how it differs from risk capacity and risk tolerance.
- Previous lesson: We explained the expected return formula and showed how to make expected return calculations.
If you’ve enjoyed this lesson, we suggest you check out our other courses and tutorials as well. For questions or comments, you can reach us here.

