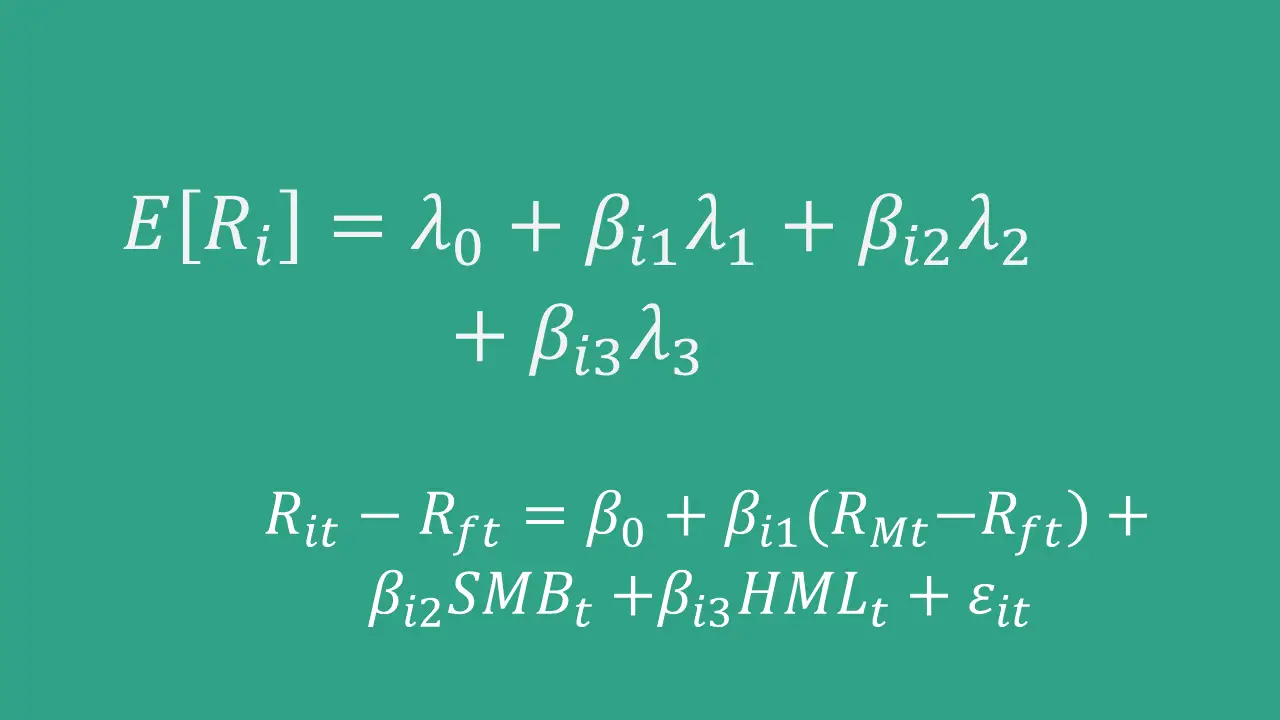Arbitrage pricing theory (APT) is an asset pricing model developed by the American economist Stephen Ross in the mid-1970s. While the capital asset pricing model (CAPM) posits a single systematic risk factor, which is the market risk, arbitrage pricing theory accommodates multiple risk factors. As such, APT has been the driving force behind the growth of multi-factor models (e.g., the Fama-French three-factor model), which are widely used by investment professionals.
Contents
Arbitrage pricing theory formula
The Arbitrage pricing theory formula with n systematic risk factors is as follows:
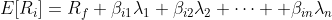
where E[Ri] is the expected return on asset i, Rf is the risk-free return, βij measures asset i‘s exposure to the jth systematic risk factor and λj is the risk premium (i.e., E[Rj] − Rf) on the same factor. βijs are commonly referred to as factor betas or factor loadings.
We can compare this formula to the CAPM formula, which is:

where E[Ri] is, again, the expected return on asset i, βi captures the asset’s sensitivity to market risk, E[Rm] is the expected return on the market portfolio, and Rf is the risk-free rate of return. So, we can see that the CAPM is a special case of APT with one factor where that factor is the market risk and E[Rm] − Rf is the market risk premium.
Chen, Roll, and Ross model
To give you a practical example of the APT formula, let’s consider Chen, Roll, and Ross model, which is an early empirical implementation (see full reference at the end). This is a multifactor model based on macroeconomic variables. According to this model, the expected return on a risky asset is:
E[Ri] = Rf + βi1λ1 + βi2λ2 + βi3λ3 + βi4λ4 + βi5λ5 + βi6λ6
where λjs are based on the following factors:
- return on the market index
- monthly growth rate in industrial production
- change in expected inflation
- unanticipated inflation
- unanticipated change in the risk premium
- unanticipated change in the term structure
Based on their empirical estimation of this model, they find that (i) the return on the market index isn’t priced (i.e., λ1 is not statistically different than zero at conventional levels), (ii) industrial production and changes in the risk premium have positive risk premia (i.e., λ2>0 and λ5>0), and (iii) the remaining macro variables have negative risk premia associated with them (i.e., λ3<0, λ4<0, and λ6<0).
Arbitrage pricing theory assumptions
Every model is a simplification of reality based on a set of assumptions, and asset pricing models such as APT and CAPM are no exceptions. CAPM has a restrictive assumption that investors are mean-variance optimizers. This means that they choose portfolios based on their expected return and variance only. In reality, investors may care about other features of portfolios as well (e.g., skewness, kurtosis, etc.). Arbitrage pricing theory has the advantage that it does not rely on this assumption of mean-variance optimization. It mainly requires that there are a sufficient number of sophisticated investors who monitor markets to exploit arbitrage opportunities. Their presence ensures that asset mispricings are short-lived, and prices satisfy the no-arbitrage condition most of the time.
One drawback compared to CAPM is that APT may not hold as well for individual assets (e.g., stocks) as diversified portfolios. This is because individual assets carry a large amount of unsystematic risk, in which case the no-arbitrage condition is harder to satisfy.
Summary
Since its development in the mid-1970s, the arbitrage pricing theory has been highly influential in financial markets, fuelling the growth of factor models, which found extensive use within the investment management industry. It is a very flexible model, which can allow for any number of systematic factors.
One caveat is that it does not tell us what those factors should be. It is the investor’s task to choose the factors, and most investors rely on established multi-factor models. In contrast, CAPM offers a theoretical foundation for considering market risk as the sole systematic risk factor.
Further reading:
Chen, Roll, and Ross (1986) ‘Economic Forces and the Stock Market‘, The Journal of Business, Vol. 59(3), pp. 383-403.
Ross (1976) ‘The arbitrage theory of capital asset pricing‘ Journal of Economic Theory, Vol. 13(3), pp. 341-360.
What is next?
This lesson is part of our free course on investments.
- Next lesson: We will move on to the topic of performance evaluation by introducing Jensen’s alpha as a risk-adjusted performance measure.
- Previous lesson: We covered the capital asset pricing model, which is another important asset pricing model.
If you enjoy reading our content, you can support us by spreading the word. And, if you have any questions or suggestions for us, you can reach us here.