Jensen’s alpha is a popular performance evaluation metric, which was developed by the American financial economist Michael Jensen in the late 60s. It is a risk-adjusted performance measure (other examples include the Sharpe ratio and Treynor ratio) and is theoretically linked to the capital asset pricing model (or the CAPM).
Contents
Jensen’s alpha formula
We can state the Jensen’s alpha formula as follows:
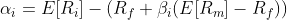
where αi is the Jensen’s alpha for asset i, E[Ri] is the expected return on asset i, βi is the beta of asset i, Rf is the risk-free rate of return, and E[Rm] is the expected return on the market portfolio. Note that this measure is forward-looking as it is based on expected returns. You can also compute the realized Jensen’s alpha, which is backward-looking, using the same equation but with historical returns instead of realized returns.
Example
Let’s suppose an actively-managed fund generated a return of 20% last year. The market return and the risk-free rate were 10% and 2% over the same period, respectively. Furthermore, the fund’s beta is 1.4. Then, we have:
αi = 20% − [ 2% + 1.4 (10% − 2%) ]
= 20% − [ 2% + 11.2% ] = 6.8%
Jensen’s alpha calculator

In order to use our Jensen’s alpha calculator, you need to enter the asset’s return, its beta, and the market return. Note that the calculator works with both expected returns and historical returns over a single period.
Relationship with the CAPM
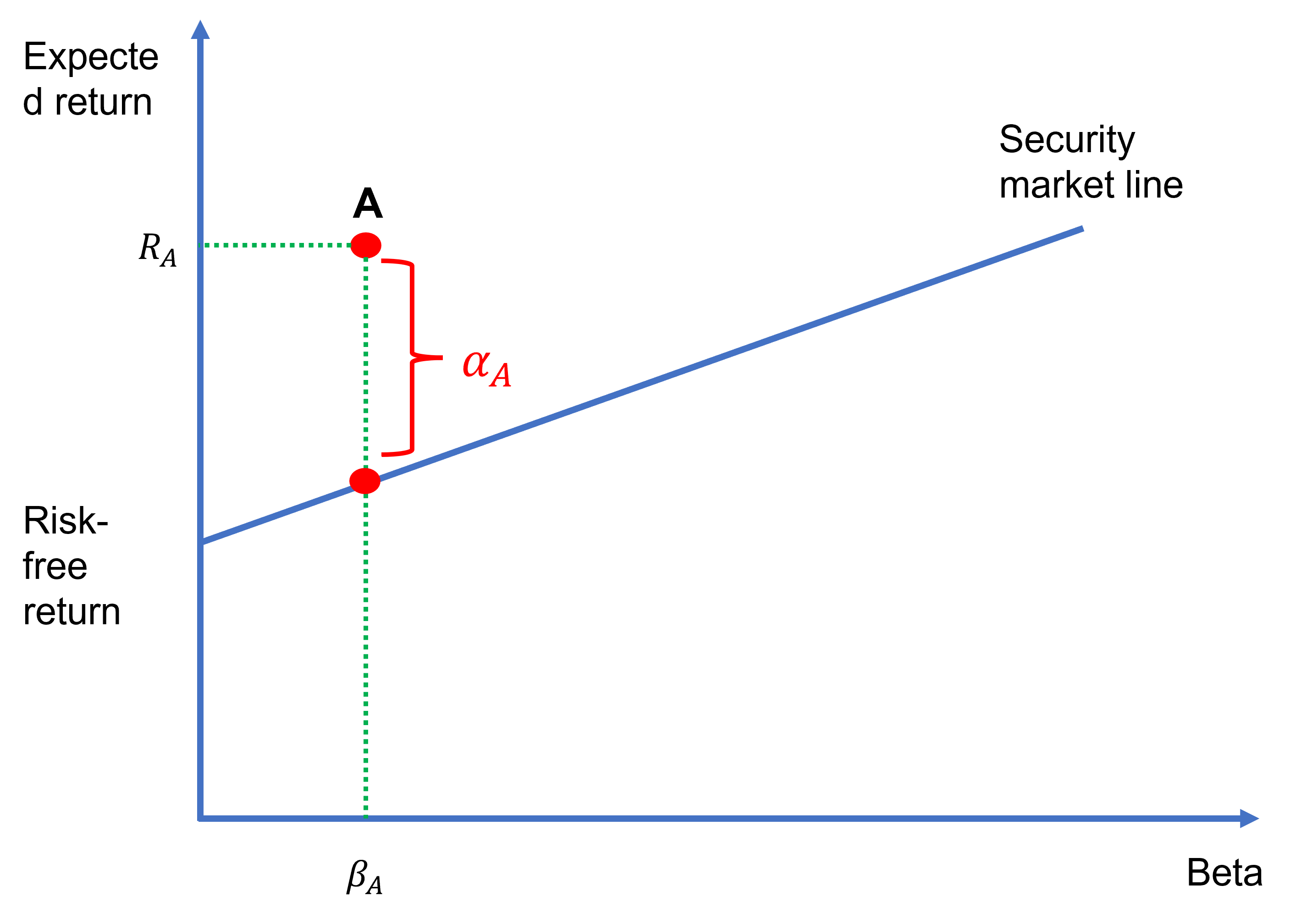
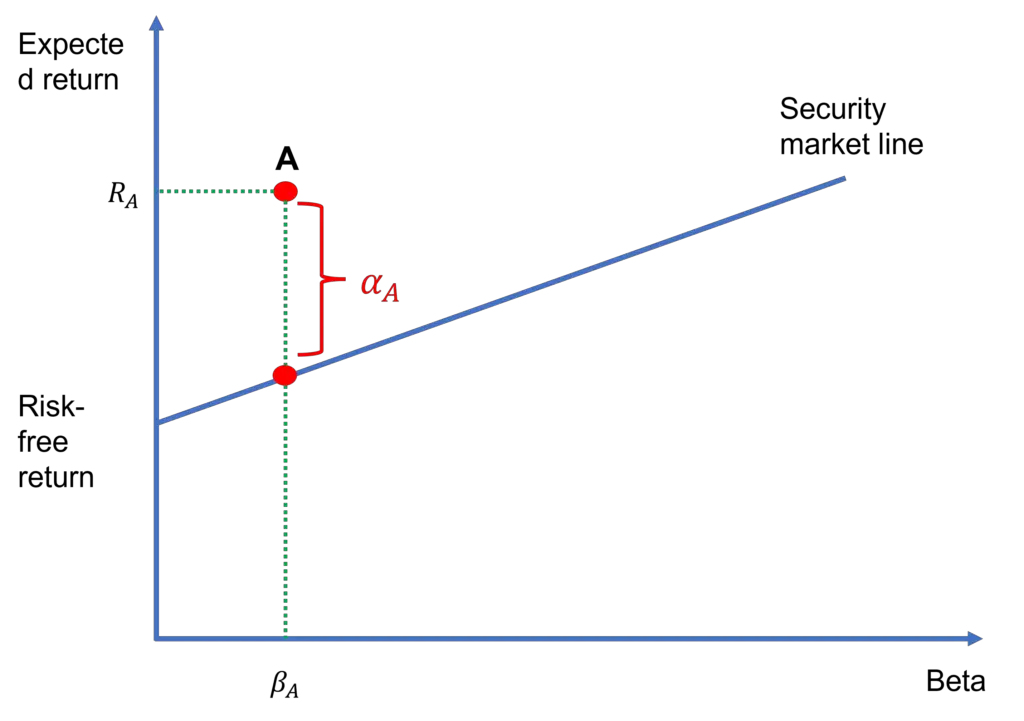
We can think of an asset’s Jensen’s alpha as the difference between its return and what its return should be according to the CAPM. In other words, if an asset’s return is exactly as what the CAPM predicts, then its Jensen’s alpha is zero: αi=0. If it exceeds the level predicted by the CAPM, αi is positive. And, if it falls short of CAPM’s prediction, αi is negative. This is illustrated in Figure 1 as follows.
Figure 1 plots the security market line (SML), which is simply a depiction of the CAPM equation. The figure also shows asset A. The Jensen’s alpha for asset A (αA) is simply the vertical distance between this asset’s return and the return of another asset that has the same beta as A but that lies on the SML.
Clearly, asset A has a positive αA. That is, its return is higher than an asset that has the same beta and that lies on the SML. In general, for any risky asset such as a stock, mutual fund, etc., αi is positive if the asset lies above the SML and negative if it lies below the SML. Of course, the asset’s αi would be zero if it lied on the SML.
In practice, the realized alpha for a risky asset over a specific period can be calculated by regressing the excess returns on the risky asset on the excess market returns. In this case, αi is the intercept estimate of this regression model. It would be important to test its statistical significance to check whether or not it is statistically different than zero at conventional levels.
Summary
In this lesson, we have discussed the Jensen’s alpha formula αi and its link to the CAPM. Note that αi can also be calculated based on multi-factor models such as the Fama-French three-factor model.
Regardless of the specific asset pricing model used, a positive αi signifies outperformance and a negative αi implies underperformance on a risk-adjusted basis. Actively managed funds exist to provide their investors with a positive αi. And, the more positive the αi is, the better the fund’s performance is.
As a final word, it might be worth highlighting that the fact that a stock or fund yielded a positive αi in the past (say the last five years) would by no means guarantee that the same asset would yield a positive αi in the future as well.
Further reading:
Jensen (1968) ‘The Performance of Mutual Funds in the Period 1945-1964,’ The Journal of Finance, Vol. 23 (2), pp. 389-416.
What is next?
This lesson is part of our free course on investments.
- Next lesson: We will introduce another popular risk-adjusted performance measure: the Sharpe ratio.
- Previous lesson: We focused on the arbitrage pricing theory (APT), highlighting its links to factor models.
If you enjoy reading our content, please spread the word by sharing our posts with others who you think might benefit from reading them. Also, feel free to get in touch with us to let us know your views.